In electrochemistry, a specific potential is applied upon a working electrode in order to let a specific reaction occur. The potential of a working electrode should be always exactly specified. That is the reason requiring a reference electrode as reference of the potential.

Typically a small glass tube (sometimes tubular Teflon for anti-corrosion) is used as the container for these three components. The frit is located at the end of the tube for electric contact with test solution. Requirement of a reference electrode is a long time stability in constant indication of potential. For that, electric current should not be allowed to flow through the reference electrode. Since the current flow may cause a drift of potential, a reference electrode is desired to be connected to a high impedance circuit. Potentiostat has a reference electrode connecting terminal which is high input-impedance terminal. Hence, current flow is strictly limited through a reference electrode.
Although only connecting a platinum wire, which is immersed in a test solution, to the reference terminal of potentiostat makes electric contact with the test solution, so called pseudo-reference electrode, but that could not guarantee the stability or reproducibility of potential measurement. It might be worthy to note that reproducible measurement is possible only by connecting a reliable reference electrode.
Although electric current does not flow through reference electrode, internal impedance of reference electrode itself is better as small as possible. As potentiostat is an automatic control system, involving a high impedance component in the feedback loop results in decrease of response rate (in another words, narrowing of band-width), then it destabilizes to oscillation. It is necessary to avoid the formation of deposit in the frit located in the end of reference electrode, which might result in extremely high impedance of the reference electrode.
Standard hydrogen electrode (SHE) is a primary standard of potential, but it is not necessarily convenient for daily use because of troublesome handling of hydrogen gas. Instead of SHE, as secondary reference electrodes, saturated calomel electrode (SCE), silver-silver chloride electrode (SSCE) and reversible hydrogen electrode (RHE) etc are well known and used.
The reason is that a redox reaction on the electrode surface occurs reversibly and equilibrates all the time as shown below.
SHE H2 ⇔ 2H+ + 2e- (0V)
SCE Hg + Cl- ⇔ 1/2Hg2Cl2 + e- (+0.24V)
SSCE Ag + Cl- ⇔ AgCl + e- (+0.20V)
The electrode, which is able to consist of a redox pair in equilibrium is called a reference electrode. The potential of a reference electrode is not able to be changed externally so that it is called non-polarizable electrode. On the contrary, platinum, gold and carbon, of which potential are able to be changed externally are called polarizable electrodes and are used as working or counter (auxiliary) electrodes.
As the relative potentials among the various reference electrodes are fixed and well-known, it is of significant meaning that the comparison between experimental data obtained in even if different places and times is able if the reference electrode used is specified.
A reference electrode is used as in equilibrium so that the net-current in circuit connected to the reference electrode is desired to be zero. Or rather it must be used under zero current. Connecting terminal for reference electrode in potentiostat has extremely high input impedance so that it is impossible for current to flow through the reference electrode. That is one of the important functions of potentiostat.
The most used reference electrode nowadays is silver-silver chloride electrode (SSCE). SSCE is environmentally friendly compared to calomel electrode using mercury and its salt. Its stability, reliability and reproducibility are also sufficient.
The reaction on SSCE is shown as below.
Ag + Cl- ⇔ AgCl + e- (+0.20V)

The electrode potential of above reaction is given as follows.
E = E0Ag+ + (RT/F)ln aAg+ eq.(1)
Substitution of the activity of silver ion with the solubility product constant of AgCl , KsAgCl results eq(1) into following equation (2).
E = E0Ag+ + (RT/F) ln KsAgCl - (RT/F) ln aCl- eq.(2)
Using literature values of E0Ag+ and KsAgCl ( E0Ag+=0.7991 V, and KsAgCl = [Ag+][Cl-] = 1.6×10-10), well-known equation (3) is obtained.
E = 0.222 - (RT/F) ln aCl- eq.(3)
aCl- is the activity of chloride ion in internal solution of the electrode. So, the reference potential of SSCE depends on the activity of chloride ion in addition to temperature. An increase of the activity results in a cathodic shift of the potential. Hence, keeping internal chloride concentration to constant is important to obtain reproducible results.
Reference potential of saturated SSCE(in saturated KCl solution) is 0.197 V at 25℃ versus standard hydrogen electrode(SHE). Electric contact of reference electrode with test solution is performed through the frit which permits mutual transfer between the internal solution and the test solution. Hence, dilution of the internal solution and contamination of the test solution provides a possible significant trouble sometimes.
Instead of KCl, sometimes NaCl is chosen as an internal electrolyte. When perchlorate anion is involved in test solution, NaCl is often employed as internal electrolyte because of the low solubility of potassium perchlorate compared with sodium salt. Deposition of potassium perchlorate within the frit may cause serious trouble like large increase of reference electrode impedance.
A main reason of using KCl is that potassium cation and chloride anion have almost identical mobility so that the liquid junction potential at the liquid interface composed of these ions is minimized. While, the liquid junction potential for the case using NaCl as internal electrolyte may become rather considerable. Which one is better choice might depend on a compromise among practical convenience.
Management of reference electrode is important, otherwise resulting in shift of reference potential. Reference electrode should be kept in solution of the same composition of internal solution, while it is not used. Contamination or deposition within the frit due to external substances should be excluded, otherwise resulting in big trouble such as oscillation of potentiostat caused by external noise etc.
For the check, if the reference electrode is properly, you can measure comparing with the new one of the same type.
Since the reference electrode in the cell is the same, the ideal potential difference is 0 Volt, however in a practice a small potential difference will occur.
It can be used if the potential difference, between the electrodes, is within 0 ± 20 mV.
For the measurement, immerse the reference electrode in 3 M NaCl solution or saturated KCl solution, and then measure the potential difference between both them using a voltmeter.
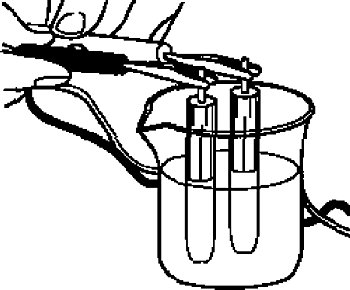
Reference: Potential for difference type of the reference electrode.
Equilibrium reaction shown below takes place in calomel electrode.
Hg + Cl- ⇔ 1/2Hg2Cl2 + e- (1)
The electrode potential is given as following equation.
E = E0Hg22+/Hg + RT/2F ln Ks(Hg2Cl2) - RT/F ln aCl- (2)
Early two terms in right side of equation (2) is replaced to E0Hg2Cl2/Hg which is calculated to be 0.273V from the literature values of redox potential
(E0Hg22+/Hg = 0.7960V) and the solubility product constant (Ks(Hg2Cl2)=2×10-18).
Replacing again E0Hg2Cl2/Hg to E0, the equation (3) is obtained, which is familiar formula involving the activity of chloride ion.
E = E0 - (RT/F) ln aCl- (3)
Although a small discrepancy in above calculated value exists, E0 is known as 0.268 V for standard potential at 25°C. The electrode potential depends on the concentration of chloride ion as like silver-silver chloride electrode. It is 0.280 V at 1M KCl and 0.241 V at saturated KCl which is so often called as SCE as abbreviation of Saturated Calomel Electrode.

The reference potential of SCE is 0.241 V(at 25°C) , because of increased activity of chloride ion in internal solution of saturated KCl (ca. 4.8 M). In addition to the chloride concentration dependence of potential, the temperature dependence of potential is about -0.5 mV per degree. Except for SCE, the reference potentials are 0.280 V and 0.334 V for 1 M KCl and 0.1 M KCl, respectively. The higher the concentration of KCl is, the larger the temperature dependence of the potential is.

We often receive the question of "Is SCE usable for experiment in organic solvent?" . Answer is "Yes". However, in the case when you dislike a contamination with water or chloride ion, you are recommended to use a salt bridge, in which both the same organic solvent and electrolyte used in your test solution is contained. Even so, you have to pay attention the fact that a rather large junction potential between SCE and the salt bridge still remains unknown. In addition to that, considering a growing risk of deposition in the frit, it might be better to use a reference electrode for non-aqueous solvent(such as Ag-Ag+ in organic solvent ) or pseudo-reference electrode (such as Pt wire), then refer to the internal standard such as ferrocene.
Usage of pseudo-reference just connecting to the reference terminal of potentiostat is recommendable from the stand point of low impedance.
NHE(Normal Hydrogen Electrode)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・0mV
SCE(Saturated Calomel Electrode)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・241mV
SSCE(Sodium Saturated Calomel Electrode)・・・・・・・・・・・・・・・・・・・・・236mV
Ag/AgCl(SaturatedNaCl)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・201mV
Ag/AgCl(Saturated KCl)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・198mV
Hg/HgSO4(Saturated HgSO4)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・616mV
Cu/CuSO4(Saturated CuSO4)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・300mV
In this section, we present the other reference electrode when you do not want to use the typical reference electrode (Ag-AgCl or calomel electrode) already mentioned. For example, you may be discouraged to use it in the cases that your test solution has to be kept away from a contamination with chloride ion or it is strong alkali or strong acid etc. In those cases, you have a choice of mercury-mercuric oxide (Hg-HgO) reference electrode for alkaline solution and mercury-mercurous sulfate reference electrode for neutral or acidic solution.
This is used for strong alkaline solution. It is utilized the equilibrium reaction between mercuric oxide layer formed on mercury and hydroxide anion in alkaline solution as internal solution. Consecutive reactions are shown below.
Hg ⇔ Hg2+ + 2e- (1)
HgO + H2O ⇔ Hg(OH)2 ⇔ Hg2+ + 2OH- (2)
The electrode potential for the reaction (1) is given shown below as equation (3).
E = E0Hg/Hg2+ + (RT/2F) ln aHg2+ (3)
Since the activity of mercuric ion is given by using the solubility product constant as aHg2+ = Ks(Hg(OH)2) /(aOH-)2, equation (3) is replaced to equation (4).
E = E0Hg/Hg2+ + (RT/2F ) ln Ks(Hg(OH)2) - (RT/F ) ln aOH- (4)
As described in the section of silver-silver chloride, the standard potential of the reference electrode utilizing highly insoluble salt depends on significantly its solubility product constant.
Using E0Hg/Hg2+ = 0.8537 and Ks(Hg(OH)2) ≃ 10-25, equation (4) is finally given as below.
E = 0.116 - (RT/F ) ln aOH- (5)
As the internal electrolyte, 0.1 M, 1 M, 3 M and saturated solution of NaOH or KOH are employed. Saturated solution of Ca(OH)2 or Ba(OH)2 are sometimes used because of its low solubility compared with NaOH or KOH. Lower OH- activity of these alkali earth solution is favorable for use of glass container and raises the standard potential a little bit upward. The standard potentials of 1 M KOH, 1 M NaOH, saturated Ba(OH)2 and saturated Ca(OH)2 are 110 mV, 113 mV, 146 mV and 192 mV, respectively.
The electrode reaction and the electrode potential are shown as follows.
Hg + 1/2SO42- ⇔ 1/2Hg2SO4 + e- (6)
E = E0Hg/Hg22+ + (RT/2F) ln aHg22+ (7)
The equation (7) is replaced by using the relation between the activity of mercurous ion and the solubility product constant Ks(Hg2SO4),
(Ks(Hg2SO4) = [Hg22+][SO42-]) as follows.
E = E0Hg/Hg22+ + (RT/2F ) ln Ks(Hg2SO4) - (RT /2F ) ln aSO42- (8)
Putting E0Hg/Hg22+ = 0.7960V(25°C) and Ks(Hg2SO4) ≃ 7×10-7, into equation (8), the final form is shown as below.
E = 0.6125 - (RT/2F ) ln aSO42- (9)
The reference potential is considerably positive compared to that of calomel electrode reflecting rather large solubility of mercurous sulfate. Saturated K2SO4 or 1 M H2SO4 are used as the internal electrolyte.
This reference electrode is an appropriate choice for the case to avoid a contamination of chloride ion.
Line-up of those kinds of electrode are available from BAS Japan as RE-61AP for Hg-HgO electrode and RE-2CP for Hg-Hg2SO4 electrode.
| &refx(): File not found: "RE-6AP_b.png" at dir "xdata/ref_electrode/"; RE-61AP |
&refx(): File not found: "RE-2CP_b.png" at dir "xdata/ref_electrode/"; RE-2CP |
In this section, we describe about a reference standard applicable for usage in organic solvent. The reference electrodes already mentioned for aqueous solvent are also usable in organic solvent by placing an appropriate salt bridge between test solution and aqueous reference electrode. As a matter of fact, the description of redox potential referred to SCE or Ag-AgCl is found in a lot of literature. In many of them, junction potentials between aqueous reference electrode and organic test solution have been ignored. So it is not always an easy task to compare our results with literature value or to evaluate discrepancy among literatures. Hence, considering inevitable contamination due to water and/or chloride ion and involvement of extra unaccountable junction potential, it might be better not to use aqueous reference electrode for non-aqueous study.
Ag+-Ag electrode is used in experiment for non-aqueous solvent in general. The basic structure of electrode is similar to Ag-AgCl electrode. Silver wire is inserted into a glass tube containing small amount of silver salt, organic solvent and large amount of electrolyte. Acetonitrile is employed as an internal solvent in most cases. The solvent used for an analyte solution is also usable in many cases. The electrolyte is selected from the combination of tetraalkylammonium R4N+ (R=methyl, ethyl, propyl and butyl etc.) as cation and perchlorate ClO4-, hexafluorophosphate PF6- and tetrafluoroborate BF4- so on as anion.
It is better for the larger concentration of electrolyte to be used as much as possible within solubility limit (typically more than 0.1 M). In addition to that, small amount of silver salt (0.01 M, the salt with NO3-, ClO4-, PF6- and BF4- etc.) is solubilized as Ag+ source. The long-term stability and reproducibility of this electrode is not always good. In addition to that, the reference potential depends on kinds of solvent. So relying upon Ag-Ag+ electrode only is not sufficient for the specification of redox potential of test compound. IUPAC (International Union of Pure and Applied Chemistry) recommends to use the internal standard such as ferrocene or bisphenyl chrome(I). The redox potential of these compounds does not depend so much on the kinds of using solvent. The reason is inferred that the redox site of Fe2+/3+ in ferrocene or Cr+1/0 in bisphenylchrome(I) are efficiently screened from influence of surrounding medium due to as sandwiched by pentadienyl ring or phenyl ring, respectively.
Even when you use Ag-Ag+ reference electrode, you should refer to the redox potential of ferrocene or bisphenylchrome as conventional potential standard. Bisphenylchrome(I) is used as tetraphenylborate salt. The redox potential of ferrocene is about +0.7 V on SHE scale, redox potential of bisphenylchrome(I) is -1.15 V on ferrocene scale (about -0.45 V on SHE scale). Both simultaneous measurements by as-contained in test solution or post-measurement by after-addition are viable. The virtue of employing internal standard is that a relative comparison with the potential on SHE scale becomes feasible via ferrocene scale.
Although the redox potential of Ag-Ag+ (Ag+ + e- ⇔ Ag) in aqueous solution is known as 0.7991 V vs SHE, this value changes largely in organic solvent due to difference of solvation energy toward mainly cation. For example, it is 0.65 V in dichloromethane, 0.41 V in tetrahydrofuran, 0.04 V in acetonitrile. As the oxidant (cation) is stabilized in polar solvent, the redox potential shifts toward negative direction depending on the extent of destabilization by the kind of solvent. Thus, non-aqueous Ag-Ag+ reference electrode might be not appropriate for specification of redox potential of analyte compound and just used as reference electrode. It might be recommendable that redox potential should be referred to the internal standard in your paper. Dimethylformamid(DMF) and dichloromethane are inappropriate from the view point of reactivity or solubility of Ag+ ion.
Pseudo-reference electrode is a way to be considered. It is just to connect Pt wire immersed in test solution to reference terminal of potentiostat (Because potentiostat has a reference electrode terminal which must be connected) which must not remain to be open. Although the specification of potential is not guaranteed, Pt wire might be a choice, considering low impedance of it and elimination of junction potential. Of course, it is needed to describe about the internal reference used in the case for publication.
When non aqueous reference electrode is immersed directly into the sample solution, supporting electrolyte of the reference electrode internal solution, present in the IPPG (Ion Permeability Porous Glass) porous, could be dissolved in the sample or reacts with the measured sample, and it could be the reason of the clogging of the porous. Using the sample holder, as shown in the example below, it will prevent that it happened.
Fill the sample holder with an electrolyte solution, and check that there is no air bubble over the IPPG liquid junction. If there is some bubble, flick to take them out. The presence of the bubble, makes that the ion permeability will differ, and it could change the applied potential.
Then, set the non aqueous reference electrode into the sample holder. Set the position of the reference electrode moving the o-ring. Filling the sample holder with the same supporting electrolyte solution, as the reference electrode, the applied potential will be kept constant.
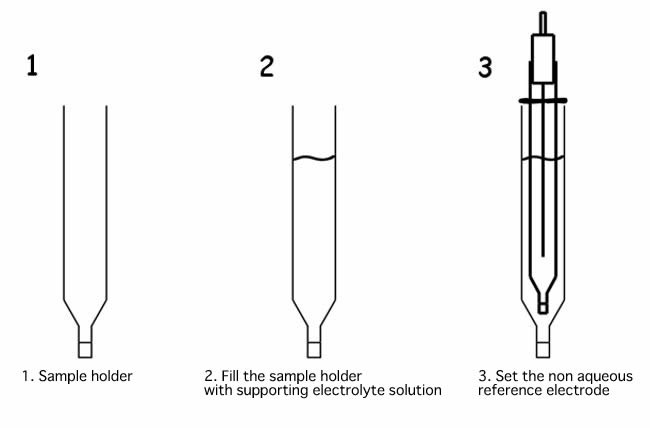
If you want to use the reference electrode in such way, use the SVC-2 Voltammetry cell. And, when a new sample holder will be used, keep immersed in a solution overnight before use. Permeating the solution to the porous of IPPG, increases the permeability of the ion through them, making able to carry out the cyclic voltammetry experiments.
Primary standard of electrode potential is standard hydrogen electrode (SHE), which is composed of Pt electrode of high surface area immersed in acidic solution containing proton and hydrogen gas of standard activity (H+ and H2 of activity = 1) (Figure1 shown below). Pt electrode is utilized due to its high activity for redox reaction of hydrogen. The surface of Pt electrode is platinized in order to enhance the activity further by increasing surface area. To keep H2 content in steady state, hydrogen gas has to be continued to flow through internal solution by bubbling.
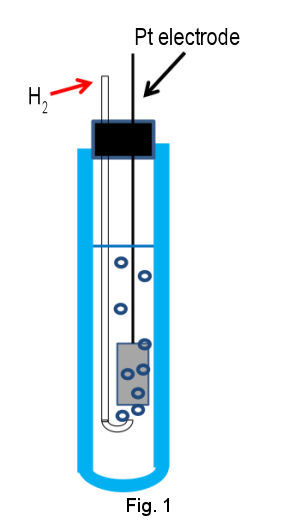
The electrode potential depends on proton concentration (activity, a H+) and hydrogen partial pressure (p H2) according to eq (2).
However, SHE is not convenient in practical use. That is a reason why the other electrodes already mentioned are employed for daily use. Even if using the other reference electrode, there are so many cases to report on SHE scale after converting experimental value to on SHE scale using well known difference. For example, in the case using SCE, SHE = SCE + 0.241 etc.
There is a convenient method to obtain approximate SHE during short time span, so called reversible hydrogen electrode (RHE), in other words, relative hydrogen electrode. Commercial available one (RHEK), which is available by BAS Japan is utilized for temporary use. It basically consists of producing hydrogen gas in the reference electrode itself in every time of experiment by user. The evolved hydrogen on platinum electrode in strong acid solution (1.2 M HCl or 0.5 M H2SO4) by cathodic polarization is stored temporally in the reference electrode chamber. Although its purpose is a use in strong acid analyte solution, it is also usable in a neutral solution by joint use of double junction chamber. It is certified by the comparison with SCE and Ag-AgCl reference electrode that this RHE indicate approximately the same potential of SHE.
Operational procedures of RHEK are shown as follows. In the case of strong acid test solution, after siphoning up the strong acid solution into the tube of RHE main body (Fig. 2), let hydrogen gas evolve by cathodic electrolysis and store H2 in the RHE main body (Fig. 3). Then you can execute your primarily purpose after returning the working terminal which has been used on H2 evolution, to the working electrode in your test solution and exchanging the reference terminal which has been connected to counter electrode together with counter terminal(Fig. 4).
 |
 |
 |
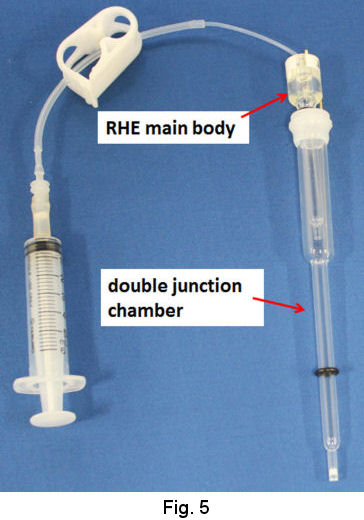
In the case of moderate acid and neutral solution or even strong acidic solution, use of double junction chamber is recommended (Fig. 5). The evolution of hydrogen gas is performed in the junction chamber by the procedure similar to that above mentioned. As the junction chamber has a frit on its tip, the junction itself can be removed from the strong acidic solution in order to be transferred to your test solution. Then, the RHE combined with the junction is used as ordinal reference electrode (Fig. 6).


Sometimes NaCl is employed instead of KCl, when perchlorate anion is involved in test solution. The reason is that the solubility of potassium perchlorate is rather low, while that of sodium perchlorate is about a hundred times higher than of potassium salt. The risk of deposition in the frit due to the low solubility of KClO4 is diminished by this precaution. Which one is employed might depend on a compromise among practical convenience.
The sample holder, which has vycor frit at the end of glass tube is available by BAS Japan. It is also usable for a salt bridge or a reference electrode.
